Quantum fourier transform
Quantum Fourier Transform (QFT) is a quantum algorithm used for performing Fourier transforms in a quantum computing environment. It is closely related to the classical Discrete Fourier Transform (DFT) and Fast Fourier Transform (FFT) algorithms but is more efficient and can be used to solve certain problems more quickly.
QFT was invented by Peter Shor in 1994 and is a fundamental part of Shor’s algorithm for factoring large integers. It is also used in the Quantum Phase Estimation algorithm, which can be used to approximate the eigenvalues of a Hamiltonian. QFT is used to transform the state of a quantum system into its Fourier transform, which is a mathematical representation of the quantum state in the frequency domain. This allows one to manipulate the quantum state to perform various operations easily. QFT is also used in quantum teleportation, quantum cryptography, and quantum computing algorithms.
Unlike the classical algorithms, the QFT is a unitary operator that is based on quantum gates instead of classical operations. As such, it can be used to solve problems related to quantum mechanical systems, such as simulating the evolution of a quantum system over time.
The main difference between the QFT and the classical algorithms is that the QFT uses the quantum phase estimation algorithm to estimate the phase of a quantum state. This allows the QFT to be used to estimate the energy eigenvalues of a quantum system, which can be used to solve particular problems more efficiently than classical algorithms.
In addition, the QFT is more efficient than the classical algorithms because it is based on quantum gates. Since quantum gates are reversible, they can be used to perform the same operation multiple times without having to start from scratch. This means that the QFT can solve problems in fewer steps than the classical algorithms. The QFT is also more efficient because it is based on quantum entanglement. This means that the QFT can solve specific problems more quickly than the classical algorithms. For example, the QFT can be used to simulate the evolution of a quantum system over time in fewer steps than the classical algorithms.
Overall, the QFT is a powerful quantum algorithm that can solve certain problems more efficiently than classical algorithms. It is based on quantum gates and entanglement and can be used to estimate the energy eigenvalues of a quantum system and simulate its evolution over time.
OPENQASM 2.0;
include "qelib1.inc";
qreg signal[4];
// Prepare signal
h signal[0];
h signal[1];
h signal[2];
h signal[3];
rz(3.14159265358979) signal[0];
// QFT
h signal[3];
cu1(-1.57079632679490) signal[2],signal[3];
h signal[2];
cu1(-0.785398163397448) signal[1],signal[3];
cu1(-1.57079632679490) signal[1],signal[2];
h signal[1];
cu1(-0.392699081698724) signal[0],signal[3];
cu1(-0.785398163397448) signal[0],signal[2];
cu1(-1.57079632679490) signal[0],signal[1];
h signal[0];
swap signal[0],signal[3];
swap signal[1],signal[2];
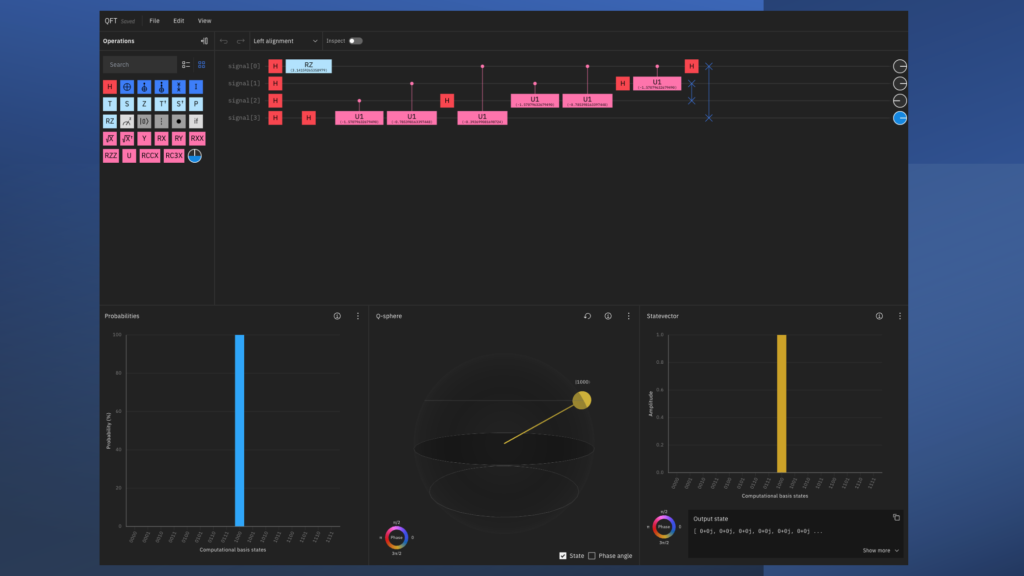
Below is the expected outcome after running above QASM code on IBM Q composer: