What is Quantum Computing?

Quantum computers use qubits, which are quantum bits that can exist in a combination of both 0 and 1. This is different from classical bits, which are either 0 or 1. These qubits can become entangled, meaning the state of one qubit will be directly linked to the state of another. This allows quantum algorithms to be much faster than traditional classical algorithms. Quantum computers can efficiently simulate quantum systems, factor large numbers, and solve linear equations.

Quantum Computing Proposed

In 1980, physicist Paul Benioff proposed a theoretical framework of a reversible Turing machine, which was the first quantum computing concept. Richard Feynman then suggested using these quantum computers to simulate quantum systems, as they would require fewer resources than classical computers. Later on, Seth Lloyd demonstrated that quantum computers could simulate any local quantum system more effectively than classical computers. Finally, David Deutsch showed that quantum computers could efficiently simulate any physical process, something classical computers could not do.

References:

Benioff: https://link.springer.com/article/10.1007/BF01011339

Feynman: https://catonmat.net/ftp/simulating-physics-with-computers-richard-feynman.pdf

Lloyd: https://www.science.org/doi/10.1126/science.273.5278.1073

Deutsch: https://royalsocietypublishing.org/doi/10.1098/rspa.1985.0070

Deutsch’s Algorithm

In 1985, David Deutsch developed an algorithm that could determine if a two-bit function was constant or balanced with a high probability of success with one call to the function. This was a major improvement over the best classical algorithm, which required two calls to determine the same result. Constant functions always return the same value no matter the input, while balanced functions return either one of two values, each for half of all possible inputs.

References:

https://royalsocietypublishing.org/doi/10.1098/rspa.1985.0070

Quantum Annealing

In 1988, researchers proposed a method of non-traditional quantum computing to find the global minimum of a function. This method, known as quantum annealing, uses quantum tunneling to build a time-dependent Schrödinger equation, which evolves the system until it reaches the solution with the lowest energy level.

References:

Apolloni et al. present a numerical implementation of quantum annealing. https://www.researchgate.net/publication/250309136_A_numerical_implementation_of_quantum_annealing

D-wave documentation: https://docs.dwavesys.com/docs/latest/c_gs_2.html

Circuit Based Quantum computation

In 1989, a model of quantum computation was developed in which initialization, logical gates, and measurements are sequentially applied to qubits to perform a specific algorithm. This model is universal, meaning it can run any quantum algorithm.

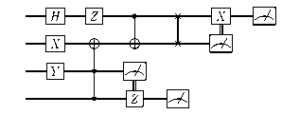
An example of a quantum computing circuit diagram is shown above. Each horizontal line represents one qubit, or quantum bit, with logical operations indicated by the boxes. The direction of time is from left to right. Operations that involve more than a single qubit are indicated by either vertical lines or boxes that span multiple qubits, each with its own symbol indicating the type of operation being applied. For example, a dot indicates that this qubit is the target of an operation that is only applied if a different qubit (shown by the circle with a cross in it) is in a specific state. Other symbols seen in the diagram include SWAP gates, measurements, and operations that depend on measurement outcomes. All operations have their own symbol, meaning any algorithm can be accurately represented as a quantum circuit diagram.

Reference: https://royalsocietypublishing.org/doi/pdf/10.1098/rspa.1989.0099

Qiskit tool: https://qiskit.org/textbook/ch-algorithms/defining-quantum-circuits.html

Deutsch-Jozsa Algorithm

In 1992, a more efficient version of Deutsch’s algorithm was proposed. This algorithm, known as the Deutsch-Jozsa algorithm, could achieve an exponential speed-up over the best classical algorithm at the time. It took a single qubit for input and produced two classical bits as output.

This diagram shows a two-qubit circuit used to implement the quantum Fourier transform. There are four gates present: two Hadamard gates, a rotation gate and a SWAP gate. Hadamard gates are used to put the qubits into a superposition, while the rotation gate (a 2×2 matrix) acts on the first qubit if the second qubit is in the ‘1’ state. To extend the circuit to include more qubits, additional copies of this circuit should be placed before the first Hadamard gate.

References:

David Deutsch and Richard Jozsa publish a paper generalizing Deutsch’s algorithm. https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.655.5997

Lecture notes; https://www.cl.cam.ac.uk/teaching/1920/QuantComp/Quantum_Computing_Lecture_7.pdf

Shor’s Algorithm

In 1994, mathematician Peter Shor created an algorithm for prime factoring that was dramatically faster than the most efficient classical algorithm of the time. The quantum Fourier transform and modular exponentiation provided speedups for Shor’s algorithm, which had implications for security based on the classical complexity of prime number factoring. This breakthrough paper set the stage for further research into building a fault-tolerant quantum computer, as well as the field of post-quantum cryptography.

Reference: https://ieeexplore.ieee.org/document/365700

A video from minutephysics that explains the workings of Shor’s algorithm. https://www.youtube.com/watch?v=lvTqbM5Dq4Q

Quantum Error Correcting Codes

In 1995, Shor and Steane developed a new way of protecting quantum computers from errors caused by noise. Classical error correction protocols couldn’t be used due to quantum mechanics, so Shor and Steane crafted quantum-compatible protocols instead. Shor’s code was able to store one logical qubit across nine physical qubits, shielding it from any single qubit error. Steane’s code was even more impressive, using only seven qubits and a Hamming code to provide the same protection. This breakthrough in quantum error correction was a major step forward in the development of quantum computing.

Shor: https://journals.aps.org/pra/abstract/10.1103/PhysRevA.52.R2493

Steane: https://royalsocietypublishing.org/doi/10.1098/rspa.1996.0136

Quantum Phase Estimation

A quantum algorithm that harnesses the quantum Fourier transform was proposed by Kitaev to estimate the phase of a quantum state and is widely utilized as a quantum subroutine.

In 1995, Kitaev proposed a quantum algorithm that took advantage of the quantum Fourier transform to estimate the phase of a quantum state. This algorithm has since become widely used as a quantum subroutine.

References:

https://arxiv.org/abs/quant-ph/9511026

https://qiskit.org/textbook/ch-algorithms/quantum-phase-estimation.html

Grover’s Algorithm

In 1996, Grover developed an algorithm that offers a twofold improvement in speed compared to the most efficient classical algorithm for unstructured search tasks. It can also be applied to classic unstructured searches where the answer can be quickly verified.

Reference: https://arxiv.org/abs/quant-ph/9605043

Grover’s algorithm for unstructured search problems, https://www.youtube.com/watch?v=EoH3JeqA55A

Topological Quantum Computers In 1997, Kitaev proposed a method of quantum computing using topological features, which would be highly resilient to errors. This method was later simplified and developed by Bravyi, resulting in the well-known surface code, one of the most widely used error correction schemes today.

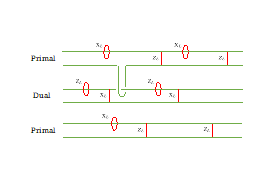
Diagrams show the definition of primal and dual types of logical qubits, which are associated with a pair of defects and measured on a Z basis. The boundary of a defect must be of an either primal or dual type. For a more detailed introduction to topological quantum computing, one can read a paper by Lahtinen and Pachos.

References:

https://www.sciencedirect.com/science/article/pii/S0003491602000180?via%3Dihub

Measurement-Based Quantum

Computing In 2003, Raussendorf and Briegel developed a method of universal quantum computing referred to as measurement-based quantum computing. It is achieved by measuring single qubits on a complexly interconnected system known as a cluster state. This approach is particularly beneficial for photonics as it is more efficient and more achievable compared to the traditional KLM scheme.

References:

https://journals.aps.org/pra/abstract/10.1103/PhysRevA.68.022312

Lecture on MBQC, https://www.youtube.com/watch?v=ipglS4nfdW0

HHL Algorithm

In 2008, Harrow, Hassidim, and Lloyd developed an efficient quantum algorithm for solving large systems of linear equations. This algorithm, known as the HHL algorithm, requires the input and output to be given as quantum states. The HHL algorithm has since been used as a component in many other quantum algorithms, such as those used to solve differential equations and in quantum machine learning.

References:

Harrow, Hassidim, and Lloyd publish a paper; In this paper describing a quantum algorithm for solving systems of linear equations. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.103.150502

A step-by-step breakdown of the HHL algorithm; https://arxiv.org/pdf/2108.09004.pdf

Variational Quantum Eigensolver

In 2014, researchers developed a hybrid quantum-classical algorithm for finding the ground state energies of a Hamiltonian. This was an important breakthrough, as this is a key problem in quantum chemistry and one of the most promising applications of near-term quantum computing. The algorithm works by using classical optimization to update the quantum algorithm’s “ansatz,” or starting point.

References:

The variational quantum eigensolver for computing the ground state energy of a Hamiltonian is described and demonstrated. https://www.nature.com/articles/ncomms5213

The Variational Quantum Eigensolver: a review of methods and best practices, https://arxiv.org/abs/2111.05176

Quantum Speed-up Of Monte Carlo Method

Quantum Speedup of Monte Carlo methods In 2015, Alexander Montanaro proposed a quantum algorithm for Monte Carlo methods that significantly improved their speed. Monte Carlo algorithms are used to estimate solutions to difficult problems using traditional methods, with applications ranging from statistical mechanics to financial mathematics. This quantum algorithm provided a near-quadratic speedup over the best-known classical algorithm at the time.

References:

Montanaro details a quantum algorithm offering a quantum speedup for Monte Carlo methods. https://royalsocietypublishing.org/doi/10.1098/rspa.2015.0301

Introduction to Classical and Quantum Monte Carlo methods for Many-Body systems; https://www.youtube.com/watch?v=qS7POodPHRA

Fusion-Based Quantum Computing

Fusion-Based Quantum Computing In 2021, PsiQuantum has developed a revolutionary quantum computing architecture that utilizes fusion-based quantum computing. Rather than using individual qubits, this technology uses a cluster state that encodes information and facilitates error correction. This approach works on any hardware, meaning it could soon be applied to a range of quantum computing projects.

References:

A team of PsiQuantum researchers introduces fusion-based quantum computation. https://arxiv.org/abs/2101.09310

Talk on FBQC: https://www.youtube.com/watch?v=vBtubw0F024